Over the years, my depth of field calculator has slowly gained complexity into what it is now. One of the additions I added more recently was to calculate the angle and field of view for the specified lens on the specified sensor.

In the last couple of months I’ve received a few questions asking why the calculated angle of view doesn’t match the actual angle of view people see in their cameras.

The short answer to this is that it’s complicated. In fact, it’s actually very complicated.

For the longer answer, read on.

The Simplest Model

My angle of view calculations, started with a very simple model. All of the details of the optics involved are ignored. Only the focal length and sensor’s dimensions are used to compute the angle of view.

Fundamentally, the angle of view is the vertex angle of the isosceles triangle formed where base is the sensor’s height, width, or diagonal, and the vertex is at a point 1 focal length away from the sensor.

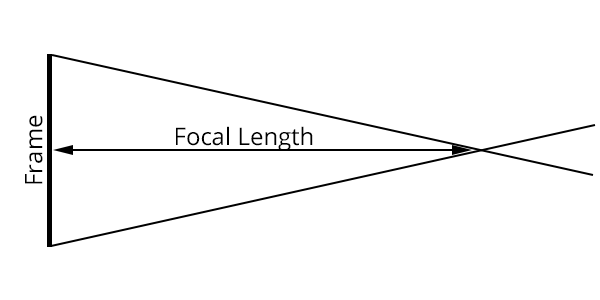
Perhaps surprisingly, this simple model actually works. Well, at least to an extent.

For any lens focused at infinity it will be pretty close. The only errors will be due to distortion and errors in the published focal length or sensor dimensions. In fact, for lens designed to not breathe while focusing, it remains accurate over most if not all of the lens’s focusing range.

However, it’s a simplistic model, and ultimately it will fail to reflect reality.

The model’s first major problem is that the effective focal length never changes as the lens focuses.

All one has to do is look at any inexpensive 50 mm prime and notice that when you focused closer than infinity, the lens shifts away from the camera. This shift is changing the effective focal length and with it the angle of view^[1].

Refining the Model: Extension Effected Focal Length

If the effective focal length changes as we focus, then the question becomes can the model be improved to take that into account?

The answer to that is that it gets complicated.

For overall extension lenses, those that move all the elements when they focus, it’s actually both possible and fairly straight forward to solve. The effective focal length is the same as the image distance, which is related to the object distance (where you’re focusing) and the focal length by the following formula.

With that we can replace the focal length in the simpler angle of view model, with the image distance/effective focal length from the above equation, and the simple model deals with focusing closer than infinity.

Only there’s a problem here.

All overall linear extension lenses, by virtue of physics, have to obey the above formula. However, internal focusing lenses do not.

Designs for internal focusing lenses can pretty much do whatever their designers want them to do. For example, cine and video lenses are designed to hold the angle of view, and thus the effective focal length, constant while focusing.

Conversely, in my experience at least, most internal focusing still photography lenses will often shorten their effective focal length (widening the angle of view) as they focus closer^[2].

Ultimately there are two problems here, at least in so far as I’m concerned as someone writing a angle of view calculator.

One is that compensating for the shift of an extending lenses, generally does the wrong thing for an internally focusing lenses. My solution to this problem was just to include both calculations, a note for which calculation to select for your lens, and a let the user pick the best value for their purposes.

The other problem is far more intractable.

Every internal focusing lens will have a different amount of effective focal length shift. This will depend entirely on what the design goals for that lens were, and how much effort the designers put into holding the angle of view constant.

Video and cine lenses almost universally tend towards having very little or no shift in focal length. Still photography lenses may have quite a lot or not so much depending on how other design considerations play out.

Since there’s no overriding formula that governs how an internal focusing lens will behave, the only way to deal with this in an angle of view calculation would be to know the behavior of a given lens design.

Moreover, in the case of a zoom lens, it’s not guaranteed that the same lens will behave the same way at either extreme of the zoom position.

For example, the published specifications for Canon’s EF 24-70mm f/2.8L II USM for field of view at 380 mm (1.25 ft) focusing distance are 554 x 369 mm at the 24 mm zoom position and 202 x 134 mm at the 70 mm zoom position.

At 24mm my calculator’s method straddle the actual results. The fixed angle of view method is about 3% too wide, and the linear compensation method is about 4% too narrow.

At 70mm both methods are too narrow, by 3.5% and 27% for the constant angle and linear extension compensation methods respectively.

Still More Complexity: Close Focusing, When Size Matters

Even ignoring that there’s no general solution for the problem of internal focusing lenses, the problems of calculating the angle of view of a lens still isn’t completely dealt with.

At long focusing distances we’ve been able to ignore the physical presences of the lens itself.

The simplest model doesn’t even “consider” there to be a lens involved at all, only a focal length to set a point for a triangle. At best, you could basically say that these simple models use the thin lens approximation.

In reality, however, lenses are anything but infinitely thin symmetrical things. They have depth. More importantly, they’re almost always not optically symmetrical and stick out in to the world they exist in.

At long subject distances, this can be ignored because the size of the lens is so much smaller than the focusing distance, that what little error it imparts isn’t material.

However, as subject distance drops, the lens’s physical size becomes larger in proportion to the focusing distance and therefore becomes a more significant factor in the calculations.

Again, mathematically it is possible to calculate the impact of the lens’s size and optical asymmetry on the effective focal length and the angle of view. However, the same problem exists here as it does with developing a general solution to the internal focusing lens problem. To calculate the error imparted by the size and asymmetry of the lens, you need to have information about specific lens designs not just something generalized.

And ultimately, as with the problem with internally focusing lenses, I don’t see a solution that’s feasible to implement without an absolutely prohibitive amount of work in testing every possible lens ever made (or at least that I want to support).

So what does all of this mean for the angle of view calculations in my DoF & AoV calculator? Well for the moment, it means that I’m going to present to angle and field of view numbers.

One (method 1) uses the simplest model, it’s best used for cine and internal focusing lenses where the angle of view either remains fixed or becomes wider as the lens is focused closer than infinity.

The second (method 2) uses the linear extension calculations to alter the effective focal length for an extending lens.

Both of these methods will still have problem at very close focusing distances. As for whether I’ll be able to solve that limitation or not, that’s still an open question that I’m investigating.